Mol. Genet. Microbiol. Virusol. vol. 3, pages 3-9, 1988, Russian
Прицип
Максимального Топологического Подобия в Молекулярной СистематикеК.М. Чумаков, С. В. Юшманов
Межфакультетская проблемная НИЛ молекулярной биологии и биоорганической химии им. А.Н.Белозерского МГУ
Проблема реконструкции конкретного хода эволюционного процесса и построения филогенетических деревьев остается неизменно актуальной задачей, поскольку эволюционная трактовка результатов исследования является имманентной частью биологического мышления. Помимо палеонтологических исследований, основным инструментом для реконструкции эволюционных схем служит сравнительный анализ тех или иных признаков с последующим построением на его основе классификационных схем и трактовкой этих схем с эволюционной точки зрения. С самого начала следует отметить, что никакой метод ни в настоящее время, ни в будущем не может гарантировать того, что предлагаемая филогенетическая схема является истинной. Однако, несмотря на принципиальную неразрешимость этой задачи, ее постановка хотя бы в приближенном виде явно осмысленна, поскольку построение гипотетических эволюционных схем служит эвристическим инструментом, стимулирующим постановку новых вопросов для конкретных исследований.
Для построения классификационных схем на разных этапах развития биологии применялись различные признаки, которые определялись методическим и методологическим уровнем соответствующего этапа. Не является исключением и молекулярная биология, в которой последнее время широкое распространение приобрели работы по сравнительному анализу последовательностей биополимеров – белков и нуклеиновых кислот. На основе такого анализа строятся классификационные схемы, которые, с одной стороны, могут быть использованы для создания систематики, а с другой – служат отправным пунктом в рассуждениях о возможном ходе эволюции.
Ясно, что задача реконструкции филогенетической схемы является более общей по сравнению с созданием классификации. Переход от такой классификации к филогенетической схеме требует дополнительных допущений и постулатов, адекватность которых должна быть предметом самостоятельного рассмотрения. В этой работе мы ограничимся только вопросом о создании классификаций и не будем затрагивать проблемы перехода от таких классификаций к эволюционным схемам. Тем не менее, имея в виду то, что получаемые схемы впоследствии будут подвергаться эволюционной трактовке, необходимо по возможности ограничить количество допущений, делаемых на этом этапе. В противном случае использованные предположения могут на последующих этапах восприниматься как результат анализа. Мы попытаемся подойти к этой задаче как с биологической точки зрения, обсудив требования, которые следует предъявлять к классификационным схемам, так и с точки зрения теории графов, и попробуем сформулировать принцип, по которому, согласно нашей точке зрения, следует строить классификационные схемы биологических объектов. Суть предлагаемого нами принципа максимального топологического подобия состоит в реконструкции дерева, имеющего структуру, в максимальной степени отражающую сведения о взаимном отношении объектов, содержащиеся в исходных данных. Реализация этого принципа стала возможной благодаря разработке количественных методов сравнения между собой структуры матриц взаимных расстояний и деревьев.
Обзор наиболее распространенных математических методов построения классификационных схем.
Прежде чем приступить к описанию предлагаемого метода, следует рассмотреть наиболее популярные в настоящее время подходы, применяемые для этой цели. Наиболее естественной формой классификации является представление данных в виде дерева. Задача может быть сформулирована так: исходя из матрицы расстояний, реконструировать наиболее соответствующее этой матрице дерево. В том случае если исходные данные могут быть представлены в виде дерева, в котором расстояния между видами в точности соответствуют расстояниям по исходным данным, то эти данные и соответствующее дерево называют аддитивными. Данные, получаемые при сравнении последовательностей биополимеров, как и подавляющее большинство других биологических данных, обычно оказываются неаддитивными. В случае биополимеров это связано с параллельными и повторными заменами, происходящими в ходе эволюции. Поэтому задача построения классификации сводится к отысканию дерева, которое максимально соответствует исходным данным. Возможны различные критерии соответствия. Первоначально в качестве критерия использовали сумму квадратов относительных отклонений расстояний между видами по исходным данным от расстояний в построенном дереве [11]. Деревья, построенные этим методом, во многом неудовлетворительны. Недостатком такого подхода является неустойчивость общей структуры дерева к незначительным локальным изменениям данных, так как зачастую удается построить несколько различных деревьев, имеющих близкие значения минимизируемого параметра. Кроме того, обычно значительная часть расстояний между видами в получаемых деревьях оказывается меньшей, чем по исходным данным. В ряде случаев длины некоторых ветвей могут оказаться отрицательными. Это показывает филогенетическую несостоятельность таких схем. Поэтому в настоящее время на практике в основном используются кластерные методы и методы, основанные на принципе максимальной экономии.Кратко опишем широкоприменяемый принцип максимальной экономии. Пусть нам известна матрица расстояний между видами из некоторого множества. Тогда деревом максимальной экономии называется дерево, удовлетворяющее следующим условиям.
1. Множество концевых вершин дерева совпадает с множеством анализируемых видов.
2. Длины всех ребер дерева не отрицательны.
3. Расстояние между двумя любыми вершинами в дереве не меньше расстояния между соответствующими им видами по исходным данным.
4. Сумма длин ребер дерева не больше суммы длин ребер любого дерева, удовлетворяющего условиям 13.
Ограничения 13 имеют ясный биологический смысл, а ограничение 4 отвечает принципу максимальной экономии
[7], утверждающему, что реальный ход эволюционного процесса осуществляется вдоль пути с наименьшим числом эволюционных событий.В настоящее время этот принцип лежит в основе большинства используемых в молекулярной биологи” алгоритмов построения классификационных схем. Но, несмотря на свою популярность, этот подход во многих отношениях неудовлетворителен.
Во-первых, принцип максимальной экономии носит несколько мистический характер, так как в неявной форме предполагает наличие у эволюции цели. Поэтому далеко не все эволюционисты принимают его. Наиболее резко эта точка зрения выражена в статье В. А. Красилова [2]: “широко практикуемое построение родословных деревьев по принципу экономии представляет по существу насилие над природой”.
Во-вторых, как недавно выяснилось, деревья максимальной экономии неустойчивы к локальным изменениям данных. Это означает, что при работе с филогениями, построенными по принципу максимальной экономии, теоретически возможна ситуация, когда, например, незначительные изменения данных об одном виде бабочек, возможно, не требующие изменения классификации
Lepidoptera, повлекут за собой изменение филогении Diptera или даже более далеких таксономических групп [14].И, наконец, в настоящее время неизвестны алгоритмы, строящие большие деревья максимальной экономии за приемлемое время. Более того, показано, что задача построения дерева максимальной экономии принадлежит к классу так называемых
NPполных задач, что делает, крайне маловероятной возможность существования таких алгоритмов [13]. Поэтому применяемые на практике алгоритмы являются приближенными, т. е. строят не сами деревья максимальной экономии, а только приближения к ним, а это во многом обесценивает сам подход.В связи с этим во многих работах для построения классификационных схем используют кластерные методы. Они вычислительно эффективны, однако не гарантируют правильности реконструкции структуры дерева даже для аддитивных данных. Иными словами, дерево, полученное кластерным методом, из матрицы расстояний между концевыми вершинами некоторого дерева, может значительно от него отличаться. Основной причиной, делающей кластерные методы непригодными для филогенетической реконструкции, является сопутствующее этим методам допущение о постоянстве скорости эволюции и ее равенстве во всех филетических линиях.
Поэтому представляет интерес разработка альтернативных принципов построения классификационных схем, которые были бы устойчивы как к неравномерности скорости эволюции, так и к локальным изменениям данных, вызванных ошибками, неизбежными при получении реальной информации, и добавлением новых данных по мере их накопления.
В любом случае эту задачу можно разбить на 2 последовательных независимых этапа: выбор оптимальной топологии (структуры) дерева и определение оптимальных длин ветвей. Очевидно, что определение общей структуры дерева является существенно более важной задачей по сравнению с определением конкретных значений длин ветвей дерева. Вторая задача решается эффективно, и основную трудность представляет 1й этап. Для решения этой задачи целесообразно в максимальной степени отвлечься от конкретных расстояний и сосредоточить основное внимание на выборе общей структуры дерева. Такой топологический подход был предложен
W. Fitch [10]. Для описания этого метода необходимо ввести некоторые топологически определения. Графом называется множество элементов, называемых вершинами, и соединяющих их ребер. При этом любые 2 вершины соединены единственной цепью ребер, т. е. в дереве отсутствуют циклы. Расстояние между вершинами – это сумма длин ребер, входящих в эту цепь.
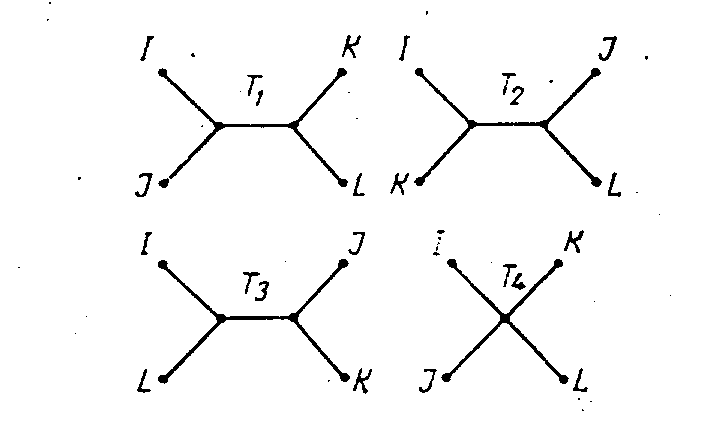
Различные варианты деревьев с 4 висячими вершинами.
В основе метода
W. Fitch лежит понятие соседства вершин дерева, для понимания которого необходимо рассмотреть условие 4 вершин, которое было впервые сформулировано Е. А. Смоленским [3] и А. К. Зарецким [11, а затем переоткрыто P. Bunneman [5, 6] и J. Dobson [9].Теорема Смоленского – Зарецкого.
Матрица расстояний между висячими вершинами дерева определяет его с точностью до вершин степени 2 и ребер нулевой длины; причем произвольная матрица расстояний может быть точно реализована аддитивным деревом тогда и только тогда, когда она удовлетворяет условию 4 вершин: для любых различных видов i, j, k, l из 3 сумм расстояний dij +dkl, dik+ djl и dil + djk 2 равны и не меньше третьей.Для того чтобы понять смысл условия 4 вершин, достаточно зафиксировать в произвольном дереве 4 различные вершины
i, j, k, l и рассмотреть поддерево Т (i, j, k, l), образованное простыми цепями, соединяющими вершины i, j, k, l между собой. Легко видеть, что оно с точностью до вершин степени 2 совпадает с одним из деревьев на рисунке. Пусть для определенности оно совпадает с Т1. Тогдаdij+dkl < dik+djl = dil+djk
и общее значение сумм
dlk+djl, dii+dik больше суммы dij+dkl на удвоенную длину центрального ребра в T1. Равенство же всех 3 сумм соответствует вырожденному случаю, когда длина центрального ребра равна 0 и Т (i, j, k, l) совпадает с T4 на рисунке.Будем называть соседними те вершины в дереве, путь между которыми составлен минимальным числом эле ментов дерева: 1 внутренней вершиной и 2 ребрами. Например, на рисунке соседними будут вершины
i. j и k, l. Toгда очевидно, что на языке соотношения 4 вершин соседство означает вхождение расстояний между такими парами в левую, меньшую сумму, так как в отличие от всех остальных расстояний в расстояние между соседями не входит длина центрального (внутреннего) ребра. Итак, пользуясь соотношением 4 вершин, можно заранее, не зная дерева, определить по расстояниям между висячими вершинами, какие пары являются соседними.Очевидно, что вхождение некоей пары
i, j в отношение соседства зависит от того, в составе какой четверки видов мы рассматриваем это отношение. Определим теперь так называемую матрицу степеней соседства [15]. Матрицей степеней соседства будем называть числовую матрицу DN= || dnij || , в которой dnij равно числу четверок, в составе которых пара i, j входила в отношение соседства.Понятно, что матрицу степеней соседства можно получить как при рассмотрении дерева
, так и без него, пользуясь соотношением 4 вершин для анализа матрицы расстояний.Теорема Смоленского – Зарецкого и соотношение 4 вершин (1) справедливы для так называемых аддитивных матриц расстояний и являются необходимым и достаточным условием аддитивности. Однако, как уже указывалось во введении, в подавляющем числе реальных случаев матрицы расстояний не являются аддитивными, и, следовательно, соотношение (1) нарушается хотя бы для одной четверки. Однако очевидно, что в любом случае 4 вида можно обозначить буквами
i, j, k, l так, чтоdij + dkl £ min (dik + djl , dil + djk) . (2)
Понятно, что условие (2) является более слабым по сравнению с
dij + dkl £ dik + djl = dil + djk (3)
и поэтому называется ослабленным условием 4 вершин
[15]. Пользуясь этой очевидной аналогией с аддитивным случаем, будем попрежнему называть пары i, j и k, l, удовлетворяющие соотношению (2), соседями.W. Fitch предложил в качестве дерева, наиболее соответствующего матрице расстояний D, брать Т, для которого функция |DN (D) – DN (T)|, равная сумме модулей разности между соответствующими элементами матриц степеней соседства, минимальна.
К сожалению, на настоящий момент неизвестно никаких формальных критериев, позволяющих проверить, соответствует ли данная матрица матрице степеней соседства некоторого дерева. Поэтому даже если нам известно, что данная матрица порядка N является матрицей степеней соседства некоторого дерева, то единственный доступный нам способ нахождения такого дерева состоит в переборе всех деревьев с N висячими вершинами (т. е. уже для 10 видов необходимо перебрать 2 027 025 деревьев, если мы рассматриваем только бинарные деревья, и
4 093 236 352 дерева, если мы допускаем произвольные филогенетические деревья) [12]. И, наконец, не доказано (хотя, по всей видимости, это так), что матрица степеней соседства однозначно определяет топологию дерева, т. е., работая методом W. Fitch, мы не можем гарантировать единственного решения даже для аддитивных данных. Поэтому топологический метод W. Fitch практического применения не нашел.
Принцип максимального топологического подобия. Математический аппарат и формулировка. Чтобы решить задачу построения дерева с оптимальной топологией, необходимо создать некоторый аппарат для характеризации топологии деревьев и соотнесения между собой деревьев и матриц взаимных расстояний. W. Fitch [10] воспользовался для этого матрицами степеней соседства (см. предыдущий раздел), однако этот способ не является единственным или самым удачным. Помимо уже упоминавшейся недоказанности однозначности соответствия матрицы степеней соседства и топологии дерева, очевидно, что такая матрица лишь очень грубо характеризует топологию дерева. Существенно более тонким способом описания топологии дерева является рассмотрение соотношения 4 вершин для каждой четверки видов из набора. Из теоремы Смоленского – Зарецкого следует, что если нас интересует только топология поддерева Т (i, j, k, l) [структура Т (i, j, k, l) с точностью до вершин степени 2 и ребер длины 0), а не конкретные значения длин его ребер, то нам достаточно знать только характер соотношений между суммами dij+dkl, dik+djl,, dil+djk, а не конкретные значения входящих в эти суммы расстояний.
Оказывается, что аналогичное утверждение справедливо и для произвольного дерева. А именно, если нас интересует топология дерева, а не конкретные значения длин его ребер, то, как показано в работе Н. Colonius и Н. Schulze [8], достаточно знать не саму матрицу расстояний между висячими вершинами дерева, а только характер соотношений между суммами dij+dkl , dik+djl , dil+djk для каждой четверки висячих вершин. Иными словами, для задания топологии дерева достаточно знать топологию поддеревьев, образованных каждой четверкой (i,j,k,l).
Для этого удобно воспользоваться следующим аппаратом. Зададим на множестве всех четверок висячих вершин дерева функцию
FT следующим образом:FT (i, j, k, l) = 1, если поддерево Т (i, j, k, l) совпадает с Т1 на рисунке;
FT (i, j, k, l)=0, если поддерево Т (i, j, k, l) совпадает c Т4; во всех остальных случаях функция не определена. Из условия 4 вершин следует, что функции FT можно дать другое, эквивалентное, определение:
FT(i, j, k, l)=1, если выполнено условие (1); FT(i, j, k, l)=0, если все 3 суммы из (1) равны; во всех остальных случаях функция не определена.
Легко видеть, что FT удовлетворяет следующим условиям:
I. Если FT определена хоть на одном из наборов ijkl, klij, lkij, то она определена на всех 3 и на всех принимает одно и то же значение.
II. Если FT определена хоть на одном из наборов ijkl, ikjl, iljk, то она либо определена ровно на одном из них и равна на нем 1, либо она определена на всех 3 и равна на них 0.
Пусть заданы конечное множество видов S и не всюду определенная на множестве четверок из S функция F, принимающая значения 0 и 1 и удовлетворяющая условиям I и II. Будем говорить, что F реализуется деревом, если существует дерево Т с множеством висячих вершин S, такое, что F=FT. Н. Colonius и Н. Schulze [81 нашли критерий реализуемости функции F деревом и показали, что такая реализация единственна. Этот критерий достаточно громоздок и не дает явного способа построения дерева, реализующего функцию F. Имеется более простая характеристика реализуемых деревьями функций, лежащая в .основе описанных дальше алгоритмов. А именно справедлива следующая теорема, которую мы дадим без доказательства.
Теорема. Функция F реализуется деревом тогда и только тогда, когда из условия: F (i, j, k, l) и F (i, k, l, m) определены, следует, что F (j, k, l, m) определено и равно F (i, k, l, m).
Как было отмечено выше, функция
FT , однозначно характеризующая топологию взвешенного дерева, реализующего аддитивную матрицу, может быть найдена непосредственно из матрицы без обращения к дереву. Такая связь между аддитивной матрицей и функцией FT, характеризующей топологию реализующего матрицу дерева, позволяет говорить о топологической структуре аддитивной матрицы, определяемой функцией FT.Подобно тому, как это было сделано в
предыдущем параграфе, перейдём теперь к неаддитивному случаю и рассмотрим неаддитивную матрицу расстояний D. Определим функцию FD следующим образом: функция FD (i, j, k, l) определена тогда и только тогда, когда имеет место (2); причем FD(i, j, k, l) = 1, когда неравенство в (2) строгое, и FD(i, j, k, l)=0, когда в (2) имеет место равенство.Ясно, что функция
FD удовлетворяет условиям III. Поэтому, если 2 такие функции FD и FD' совпадают на некотором наборе ijkl, то они совпадают на всех наборах, полученных из ijkl перестановкой переменных. Это позволяет ввести для таких функций расстояния \FDFD'\ как число различных четверок (i, j, k, l), на которых FD не равно FD'.Ясно, что если функция
FD реализуется некоторым деревом, то это дерево единственное с точностью до вершин степени 2 и ребер нулевой длины, и функции FD и FT совпадают.Поэтому представляется естественным решением в качестве дерева, наиболее соответствующего матрице расстояний, брать такое дерево, для которого
|FD–FT| минимально. Величину |FD–FT |, равную числу четверок, для которых значения FD и FT не совпадают, будем далее называть топологическим несовпадением.Такой подход к задаче построения филогенетического дерева, ставящий во главе угла выбор топологии дерева, в максимальной степени отражающей тонкую топологическую структуру матриц расстояний, назовем принципом максимального топологического подобия. Преимущества такого подхода состоят в следующем.
1. В отличие от большинства применяемых на настоящий момент методов построения филогенетических деревьев принцип максимального топологического подобия не вводит никаких дополнительных допущений о ходе эволюционного процесса и скоростях эволюции.
2. Для аддитивных данных метод дает точные решения.
3. Метод нечувствителен к малым погрешностям исходных данных.
Пусть некая матрица аддитивна и пусть для какойлибо четверки
{i, j, k, 1} из 3 сумм s1=dij+dkl, s2=dik+ djl и s3=dil+djk 2, скажем s1 и s2 , равны и много больше 3й, тогда любая малая погрешность вычисления s1 или s2 или входящих в него расстояний нарушает аддитивность матрицы, но не меняет значения функции FD и, следовательно, не нарушает ее реализуемости деревом. Таким образом, класс матриц, для которых FD реализуется деревом, шире класса аддитивных матриц.4. Функция |FD–FT| дает простой объективный способ оценки соответствия структуры построенного дерева исходной матрице расстояний. Это, в частности, позволяет сравнивать между собой филогенетические деревья, построенные по разным критериям, т. е. позволяет решать задачу, которая ранее осуществлялась путем экспертной оценки специалистами.
5. Сравнение функций FD и FT на всех наборах четверок, включающих какойлибо интересующий нас вид, позволяет получить количественную оценку надежности его помещения в конкретное положение на дереве в виде величины локального топологического несовпадения. Иными словами, появляется возможность обнаруживать места в построенных деревьях, которые требуют более осторожной трактовки.
6. Метод позволяет строить классификационные схемы, учитывающие информацию о разных признаках, выраженных в единицах различной размерности. При этом будет производиться усреднение именно топологии, а не самих расстояний в нескольких исходных матрицах.
7. В отличие от топологического метода W. Fitch принцип максимального топологического подобия позволяет в явной форме получить алгоритмы построения деревьев. 2 алгоритма, реализующие принцип максимального топологического подобия, примеры, иллюстрирующие сформулированные выше преимущества, а также обсуждение биологической состоятельности предлагаемого принципа будут приведены в сопутствующей работе [4].
Литература
1. Зарецкий А. К. Успехи математ. наук. – 1965. – Т. 20. – С. 94–96.
2. Красилов В. А.Зоология позвоночных: Проблемы теории эволюции. М., 1975. С. 117147.
3. Смоленский Е. А.Журн. вычислит. математики и математ. физики. 1962. Т. 2.С. 371–372.
4. Юшманов С. В., Чумаков К. M.// Молекул. генетика. – 1988. – № 3. – С. 9.
5. Виппетап P.//J.combinat. theory. – 1974. –Vol. 178. – P. 48–50.
6. Виппетап Р. // Mathematics in Archaeological and Historical Sciences / Eds F. R. Hodson et al. – Edinburgh, 1971. – P. 387–395.
7. CavaliSforza L. L., Edwards W. F // Evolution. – 1967. – Vol. 32. – P. 550–570.
8. Colonius H., Schulze H. H. // Brit. J. math. Statist. Psychol. – 1981. – Vol. 34. – P. 167–180.
9. Dobson J.//J. appl. Probability. – 1974.–Vol. 11. – P. 32–42:
10. Fitch W. M.//J. molec. Evolut. – 1981. –Vol. 18. – P. 60–67.
11. Fitch W. M., Margoliash E.// Science. – 1967. – Vol. 155. – P. 279–284.
12. Foulds L. R., Robinson. R. W. // Combinatorial Mathematics. Berlin, 1980. Vol. 7 P. 110126.
13. Graham R.L., Foulds L.R. //Math. Biosci. – 1982. – Vol. 60. – P. 133– 142.
14. Rohlf F. J. // Syst. Zool. – 1984. –Vol. 33. – P. 341–343.
15: Sattah S., Tversky A. // Psychometrica. – 1977.–Vol. 42. – P. 319–346.
Поступила
18.06.87
Maximum Topologic Similarity Principle in Molecular Systematics
K.M. Chumakov, S. V. Yushmanov
The paper deals with the problem of phylogenetic reconstruction on the basis of comparative analysis of features. Main attention is paid to comparison and classification of the biopolymer sequences. Different approaches to this task are critically reviewed. The novel principle of construction of treelike classification schemes permitting subsequent evolutionary analysis is proposed. It concentrates on reconstruction of the tree with a topologic structure that is most close to topologic features, imprinted in the source distance matrix. Realization of this approach was made possible by development of the special formalism, enabling evaluation and comparison of topologic features of distance matrices and trees.